Reneseng

Synthesis and design of multiphase chemical and biochemical reactors

In recent years, the chemical reactor has been elevated to the position of being arguably the most important unit to optimize within a chemical process plant. The growing demand for “green products” has contributed to the rapid development of biorefineries.

Challenges

In recent years, the chemical reactor has been elevated to the position of being arguably the most important unit to optimize within a chemical process plant. The growing demand for “green products” has contributed to the rapid development of biorefineries.The fractionation of biomass and its conversion to products is the objective of recently developed chemistries which are still under research in order to be optimized. The design of contemporary biochemical reactors is mainly based on the existing experience and heuristics in conventional reactors. The diversity of feedstock, along with the complicated activity of the microorganisms used, imposes new uncertainty factors for the design of the bioreactors.

The new objectives are centered around clean technology and are namely:

1. to give as far as possible only the desired product,
2. to reduce by-products and pollution,
3. to minimize the inhibition factors, and
4. to intensify processing in order to improve economics.

This study proposes a complete superstructure framework for the full conceptual design and optimisation of different integrated biorefinery processes.

Two case studies are presented:

1. a theoretical example; the modified Denbigh reaction (Linke and Kokossis (2003) and
2. the case of a biorefinery example, the cultivation of algae for the production of lipids.

Superstructure Representation

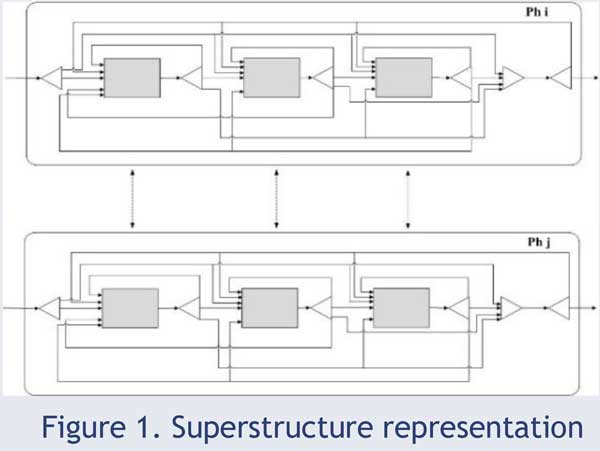
An improved version of the systematic framework for the optimization of a superstructure representation of ideal reactor units involving CSTRs and PFRs, which was firstly introduced by Kokossis and Floudas (1990), for the full conceptual design of multiphase chemical and
d biochemical reactors.

In Figure 1. the generic units of the superstructure are illustrated, which consisted of the compartments (upper blocks), which represents Phase 1 (Ph i) and shadow reactor compartments (lower blocks), which represent Phase 2 (Ph j). The horizontal connection is calculated by the mass balances. The vertical connection depends on the mass transfer between the two phases (Ph i↔ Ph j).

 

Mass Transfer

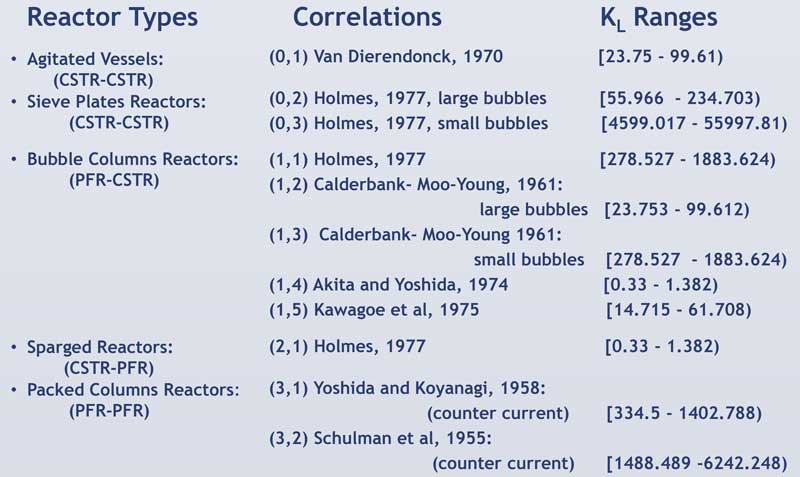
The examination the impact of different mass transfer correlations on the real design of bioreactors running different biorefineries examples based on recently developed or under research technologies using the synthesis framework embedded with appropriate mass transfer correlations for the best approximation of mass transfer between phases for each type reactor.

Optimization Technology

The synthesis framework which includes the Targeting stage, the Screening and design stage and the Analysis stage and validation, is the implementation of a generic probabilistic metaheuristic global optimization method, employing evolutionary optimisation utilising Simulated Annealing (SA) algorithm, on FORTRAN programming language, for the synthesis, design, optimization and superstructure representation of complex network reaction systems (Kokossis & Floudas, 1990).

Summary of Case Studies

Case 1) Theoretical Example
Denbigh reaction, Consisted of the following for reaction (Eq.1-4) (Mehta, 1998):

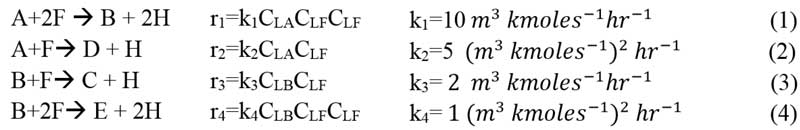
Applied for network analysis, simplifying very complex reactions such as parallel reactions, series (or consecutive) reactions, independent reactions, series-parallel reactions, triangular reactions.

Case 2) Biorefinery Example
Algae cultivation for the production of lipids. Characterized by Eq. 5, 6 (Slegers, 2014):

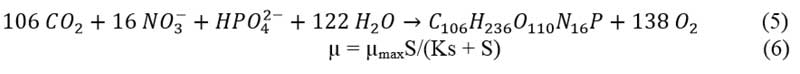
Where μ is the concentration (growth) of the biomass component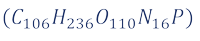and S the concentration of .

Results

(Case 1) Theoretical Example

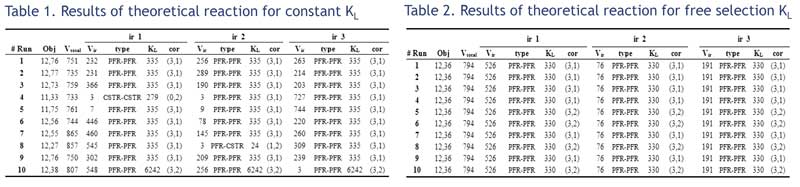
Mass transfer coefficient (KL) is set 330 for all the types of reactors.

The results presented in below (Table 1.) indicate that the reactor network does not change, resulting in an optimum configuration of PFR reactors for both phases.

KL is freely selected, restricted only by the type of reactor. PFR-PFR configuration is preferred most of the times at both cases. In this case though, alternative configurations also start to arise, with a small penalty in the objective function.

Results shown in Table 2.

Case 2) Biorefinery Example

Maximum feasible algal growth yield ratio was achieved before the point where concentration starts decreasing. The algorithm initially converged at annealing temperature 129 degrees C implying that it could undergone further optimization to give, finally, an objective value of 6.96 percent yield ratio (desired product molar flowrate over feed molar flowrate), with final annealing temperature below two degrees C.

 Conclusions and Work in Progress

• The proposed method can be applied for the synthesis, design, and optimization for both, conventional and non-conventional processes since it is fully adjustable to any

type of process.

• Reliability of the framework to adapt with flexibility and high level of accuracy reconfirmed by the results of the case studies.

• Enables reactor design of the conventional chemical processes with linear simple kinetics

• Facilitates the synthesis and design of biochemical processes with complex reaction mechanisms.

• Proven that for the algae growth and fermentation, the Michaelis –Menten kinetics (Monod equation) which applies to most biochemical processes can be accurately

simulated.

• The latest version of the framework proposed enables the real design of biochemical reactors with interactive mass transfer coefficients adapted for each case.

• The great importance of the framework is that it identifies the maximum achievable efficiency of the resulting optimum reactor network, providing useful information about:
• (1) The number and type of reactors, (2) The desired mass transfer correlation for each type of reactor, (3) The volumes of reactors, (4) The appropriate feeding, mixing, recycling and bypassing strategy and (4 )The optimalvalues of the flowrates, compositions and yields.

• Work in progress is aiming to automate this framework to enable the user the fast and easy input of reaction equations and kinetics and the feed re-characterization.

 

References 

Y. Kawase, & M. Moo?Young, 1992, Correlations for liquid?phase mass transfer coefficients in bubble column reactors with newtonian and non?newtonian fluids. The Canadian Journal of Chemical Engineering, 70(1), 48-54.
A.C. Kokossis and C.A. Floudas, 1990, Optimization of complex reactor networks: Isothermal operation. Chem. Eng. Sci., 46, 1361.
A.C. Kokossis and C.A. Floudas, 1994, Optimization of complex reactor networks: Nonisothermal operation. Chem. Eng. Sci., 49, 1037.
V. Linek, T. Moucha, F. J. Rejl, M. Korda?, F. Hovorka, M. Opletal, & J. Haidl, 2012, Power and mass transfer correlations H for the design of multi-impeller gas–liquid contactors for non-coalescent electrolyte solutions. Chemical Engineering  Journal, 209, 263-272.
P. Linke, & A.C. Kokossis, 2003, On the robust application of stochastic optimisation technology for the synthesis of reaction/separation systems. Computers & chemical engineering, 27(5), 733-758.
E.C. Marcoulaki and A.C. Kokossis, 1999, Screening and scoping complex reaction networks using stochastic optimization. G AIChE J. 45(9), 1977-1991.
L.V. Mehta, 1998, Synthesis and Optimization of Multiphase Reactor Networks, University of Manchester, Institute of Science and Technology, Dept. of Process Integration, PhD Thesis. P.M. Slegers, 2014, PhD Thesis; Scenario studies for algae production, Wageningen University, Netherlands, ISBN 978-94-G 6173-858-5.

 

Acknowledgement

The EC (Reneseng-607415 FP7-PEOPLE-2013-ITN) is gratefully acknowledged for supporting this work.

Contact

akokossis@mail.ntua.gr